Scheduling
The OS’s scheduler decides when to run which process.
Performance metrics include:
- CPU Utilization - Percentage of time that the CPU is doing useful work
(i.e. not idling). 100% is perfect.
- Wait time - Average time a process spends in the run queue.
- Throughput - Number of processes completed / time unit.
- Response Time - Average time elapsed from when process is submitted
until useful output is obtained.
- Turnaround Time - Average time elapsed from when process is submitted to
when it has completed.
Typically, Utilization and Throughput are traded off for better Response Time. Response time is important for OS’s that aim to be user-friendly. In general, we would like to optimize the average measure. In some cases, minimum and maximum values are optimized, e.g. it might be a good idea to minimize the maximum response time.
Types of Schedulers include:
- First-Come, First-Served (FCFS)
- Round-Robin (RR)
- Shortest-Job-First (SJF)
- Priority Scheduling (PS)
First-Come, First-Served (FCFS)
The FCFS scheduler simply executes processes to completion in the order they are submitted. We will implement FCFS using a queue data structure. Given a group of processes to run, insert them all into the queue and execute them in that order. Thus, our API will need the following methods and data structures and methods:
fifo_queue Q; // the queue containing the processes
add_task(proc) { // method to add a process to the queue
Q.add_tail(proc); // by inserting it at the tail end
Q.size++; // Accounting
}
reschedule() { // remove process from queue
p = Q.remove_head();
Accounting;
return p;
}
Performance Evaluation
When evaluating a scheduler’s performance, we use a Gantt Chart, which is a horizontal timeline indicating which processes are run and at what times they run starting from when all tasks are submitted and ending when all tasks have been completed.
To illustrate it, suppose the scheduler is given 4 tasks, A, B, C and D. Each task requires a certain number of time units to complete.
|
Task |
Time units |
|
A |
8 |
|
B |
4 |
|
C |
9 |
|
D |
5 |
The FCFS scheduler’s Gantt chart for these tasks would be:
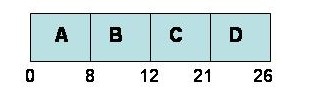
The tasks are inserted into the queue in order A, B, C and D. as shown above. Task A takes 8 time units to complete, B takes 4 units to complete (therefore, B completes at time 12), etc. Task D ends at time 26, which is the time it took to run and complete all processes.
Now we will measure the FCFS scheduler’s performance using the metrics mentioned earlier. The OS incurs some overhead each time it switches between processes due to context switching. We will call this overhead “cs”.
|
Metric |
FCFS |
|
CPU Utilization |
26/(26+3cs) |
|
Turn around time |
(8+12+21+25+6cs)/4 = 16.5 ignoring cs |
|
Waiting |
(0+8+12+21+6cs)/4 = 10.25 ignoring cs |
|
Throughput |
4/(26 + 3cs) |
|
Response |
(0+8+cs+12+2cs+21+3cs)/4 = 10.25 ignoring cs |
The average waiting time for FCFS is usually quite long and there is a possible convoy effect in which all processes wait for one big process to get off the CPU.
Shortest-Job-First (SJF)
The SJF scheduler is exactly like FCFS except that instead of choosing the job at the front of the queue, it will always choose the shortest job (i.e. the job that takes the least time) available. We will use a sorted list to order the processes from longest to shortest. When adding a new process/task, we need to figure out the where in the list to insert it. Our API will need:
sorted_list sl // sorted list data structure
add_task(proc, expected_runtime) { // method to add a process to the list.
sl.insert(proc, proc.runtime); // we input the process’s expected runtime
} // to indicate where it should be inserted.
reschedule() { // method to remove the shortest job from
return sl.remove_head(); // the list and run it.
}
For the jobs A, B, C and D used in the previous example, The SJF Gantt Chart would be:
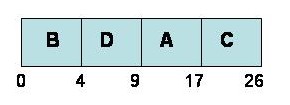
|
Metric |
SJF |
|
Utilization |
26/(26+3CS) |
|
Turn around time |
(4+9+CS+17+2CS+26+3CS)/4 = 14 ignoring CS |
|
Waiting |
(0+4+CS+9+2CS+17+3CS)/4 = 7.5 ignoring CS |
|
Throughput |
4/(26 + 3CS) |
|
Response |
(0+4+CS+9+2CS+17+3CS)/4 = 7.5 ignoring CS |
From the metrics, we see that SJF achieves better performance than FCFS. However, unlike FCFS, there is the potential for starvation in SJF. Starvation occurs when a large process never gets run to run because shorter jobs keep entering the queue.
In addition, SJF needs to know how long a process is going to run (i.e. it needs to predict the future). This runtime estimation feature may be hard to implement, and thus SJF is not a widely used scheduling scheme.
Round-Robin (RR)
RR is a preemptive scheduler, which is designed especially for time-sharing systems. In other words, it does not wait for a process to finish or give up control. In RR, each process is given a time slot to run. If the process does not finish, it will “get back in line” and receive another time slot until it has completed. We will implement RR using a FIFO queue where new jobs are inserted at the tail end.
fifo_queue fQ // FIFO queue
add_task (proc) { // method to add a task
fQ.add_tail(proc)
}
reschedule(why) { // method to remove the next process and run it
if (why == timer)
add_task(current);
set_timer(time quanta);
return fQ.remove_head;
}
RR assigns a time quanta (i.e. time slot) to each process waiting to be run. For the jobs A, B, C and D in the previous example, RR’s Gantt chart would be:
If time quanta = 3

If time quanta = 6
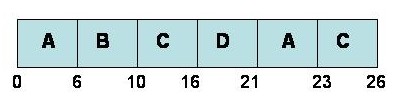
|
|
RR |
|
Utilization |
26/(26+9CS) |
|
Turn around time |
(23+16+26+21)/4 = 21.5 ignoring CS |
|
Waiting |
(15+12+17+16)/4 = 15 ignoring CS |
|
Throughput |
4/(26 + 9CS) |
|
Response |
(0+3+6+9)/4 = 4.5 ignoring CS |
The performance of RR depends on the size of the time quantum, and if the time quantum is large, RR will behave jus like the FCFS policy. In general, we want the time quantum to be large with respect to the context-switch time(cs should be around 10% of time quantum)
Priority (PRI)
A priority is associated with each process. We can think of the SJF algorithm as a special case of PRI. Processes with equal priorities may be scheduled in accordance with FCFS.
PRI (L, M, H (RR)) // using Round-Robin
fifo_queue fQ[3] // data structure
add_task(proc, pri)
fQ[pri].add_tail(proc)
reschedule(why)
if (why == timer)
add_task(current, current.pri);
set_timer(TQ);
for pri=H to L
if(fQ[pri].empty())
return fQ[pri].remove_head();
TQ=6
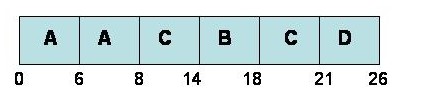
|
|
PRI |
|
Utilization |
26/(26+4CS) |
|
Response |
(0+8+14+21+4CS)/4 = 10.75 ignoring CS |
PRI (L, M, H (RR) + aging):
fifo_queue fQ[3]
add_task(proc.pri)
fQ[pri].add_task(proc)
reschedule(why)
if (why=timer)
add_task(current, current.pri);
set_timer(TQ);
for pri=M to L
for p in fQ[pri]
if now-p.list> limit
remove(p)
add_task(p, pri+1)
for pri=H to L
if(fQ[pri].empty())
return fQ[pri].remove_head();
Limit=12

Note: in this case, it’s the same as the regular pri, but that’s not always the case. For this specific case, it’s the same because C goes before D in M pri when D gets aged to M. There is a problem with PRI, which is indefinite blocking (or starvation). The technique of aging, which gradually increase the priorities of the waiting processes, is used to solve the problem.