
Iterators are fundamental to programming with C++ data types. An iterator abstracts the notion of a position in a collection, using pointer notation. Iterators are great because they allow us to write generic algorithms that work on arbitrary data structures (including subsets of data structures) with unparalleled efficiency.
We start with a concrete algorithm: finding the minimum item in a vector of integers.
int min_item(const vector<int> &v) { // our vector from last time
// ???
}
What goes in the ??? ?
int m = v[0];
for (int i = 1; i < v.size(); ++i)
if (v[i] < m)
m = v[i];
return m;
This min_item function has a precondition, namely that v cannot be empty. As
a specification comment:
/** Return the minimum item in @a v.
* @pre v.size() != 0 */
Preconditions like this are a shame; other things being equal, it’s better to have fewer preconditions, so users have less to remember. Can we write a version that works even if v.size() == 0? Yes, but if so, we probably shouldn’t return an item! So let’s return an index, rather than an item. For example:
int min_index(const vector<int> &v) {
int m = 0;
for (int i = 1; i < v.size(); ++i)
if (v[i] < v[m])
i = m;
return m;
}
If v is empty this returns 0—an index equal to the container’s size. This is a good index for nonexistent items; since indexes in C and C++ start from zero, the item “container[container.size()]” does not exist.
Here’s a very simple linked list implementation.
template<typename T> struct list_element {
T value_;
list_element<T>* next_;
};
template<typename T> struct list {
list_element<T>* head_;
list()
: head_(0) {
}
int size() const {
int i = 0;
for (list_element<T>* x = head_; x; x = x->next_)
++i;
return i;
}
T operator[](int i) const {
// Pre: i >= 0, i < size()
list_element<T>* x = head_;
while (i > 0) {
--i;
x = x->next_;
}
return x->value_;
}
};
How would we write a min_index for list?
int min_index(const list<T> &v) {
int m = 0;
for (int i = 1; i < v.size(); ++i)
if (v[i] < v[m])
i = m;
return m;
}
!!!!!!!!!!!!!!THIS IS THE SAME CODE!!!!!!!!!!!!!!!!!!
The following template, then, will work when passed either a list or a vector,
or any other data structure that supports operator[] and size:
template<typename T>
int min_index(const T &v) {
int m = 0;
for (int i = 1; i < v.size(); ++i)
if (v[i] < v[m])
i = m;
return m;
}
But is the complexity the same?
No. min_index(list) has O(v.size()2) time complexity. min_index(vector) has O(v.size()) time complexity.
The magic of C++ iterators is that they are a natural abstraction that lets us write a single max_index with the same good complexity on these fundamentally different data structures.
Let’s reason about how each of these functions actually accesses its underlying data structure.
Both run through the data structure in order, from first element to last element, using a “current position” (i) that is incremented by one each time.
Both dereference the current position (“v[i]”).
Both also remember a previous position (“m”) and dereference it (“v[m]”).
And both can see whether a position is out of range (“i < v.size()”).
It seems like the position is a shared abstraction. Here’s what we know about positions. A position can be:
In both vector and list all these operations are O(1). (Note that in the list comparing for equality is O(1), but comparing by < or > is not.)
What else has these properties? Pointers. Pointers can be:
++p.*p.p = q.p == q, p != q, p < q, etc.Pointers are also wicked fast for machines to manipulate. If our shared position abstraction uses pointer notation, then our generic algorithms can work on actual pointers, and when they do they will achieve pointer speed. And although pointer notation isn’t always easy to understand at first, it is compact and will quickly become second nature. That is why C++ iterators use pointer notation.
Let’s rewrite min_index in iterator style. We will call the result min_element. First, think about vector<>, whose iterators are basically pointers.
How do iterators affect min_element’s signature?
That leaves us with something like this:
template<T> T* min_element(const vector<T>& v) {
const T* first = v.begin();
const T* last = v.end();
T* m = first;
for (T* p = first + 1; p < last; ++p)
if (*p < *m)
m = p;
return m;
}
Notice how close this is to the code above!
What should v.begin() and v.end() return? Well, v.begin() is the first
element in the vector (index 0). And if we look at the code, v.end()
corresponds to the item at index v.size(), which, remember, doesn’t actually
exist: it is one past the end. Here’s how they look in a vector with 5
elements.

The v.end() iterator is valid for comparisons and assignments, but not for
increments or dereferences. Think of it like a fence: you can’t go beyond it.
(Like many aspects of iterators, this too comes from C and pointers. It is OK to form a pointer that points one past the end of an array, but not OK to dereference it. It is not OK to form a pointer that points two past the end, or three past the end, or one before the beginning, etc.)
However, we are using more operations than we actually need: we are comparing iterators with “<” when “!=” would suffice. Since != is faster on lists than <, let’s change the code to use the minimal set of operations.
template<T> T* min_element(const vector<T>& v) {
const T* first = v.begin();
const T* last = v.end();
T* m = first;
if (first != last)
for (++first; first != last; ++first)
if (*first < *m)
m = first;
return m;
}
Great.
What if we want to find the min element in a subsequence of some vector—like the elements between #1 and #4, say? Subsequences and sub-collections are quite useful in practice. Given a collection of animals, you might want to find the fattest panda; that’s the maximum-weight animal in the subsequence of pandas.
Iterators solve this problem cleanly for vectors. All we do is subtract code.
template<T> T* min_element(const T* first, const T* last) {
T* m = first;
if (first != last)
for (++first; first != last; ++first)
if (*first < *m)
m = first;
return m;
}
To call this on the whole vector, just call “min_element(v.begin(),
v.end())”. To call on the 3-element subsequence between elements 1 and 4,
call “min_element(v.begin() + 1, v.begin() + 4)” (only works if the vector
has 4 or more elements).
What just happened here? An iterator started out as defining a position in a collection. But once we accept this, we see that two iterators can just as easily represent a collection! This is a big idea we’ll return to.
template<T> T min_element(T first, T last) {
T m = first;
if (first != last)
for (++first; first != last; ++first)
if (*first < *m)
m = first;
return m;
}
This still works for vector. Can we make it work for list? … Well, what is a list “position”?
A pointer to a list_element with different operations. Comparison is
still pointer comparison. But incrementing is traversing a next pointer, and
dereferencing returns a reference to the list_element’s value, not the
list_element itself.
To change the operations, we need to define a new class. Here one is:
template<T> class list_iterator {
list_element *p_;
public:
T& operator*() {
return p_->value_;
}
bool operator==(const list_iterator<T>& x) const {
return p_ == x.p_;
}
void operator++() {
p_ = p_->next_;
}
};
What are list.begin() and list.end()? Think by analogy. Begin() just
points at the first element in the list: it is the same as head_. End()
should point one past the last element in the list. What’s that? Simple: a
null pointer!
template<T> class list { ...
list_iterator<T> begin() {
return list_iterator<T>(head_);
}
list_iterator<T> end() {
return list_iterator<T>(nullptr);
}
};
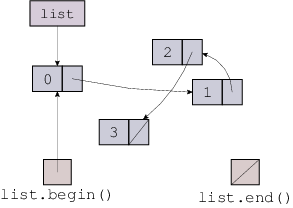
Think how this works for an iterator that starts at list.begin() above. Each operator++ traverses a next link. So after four applications of operator++, the iterator will equal a null pointer—that is, list.end()! Just what we wanted.
For the final piece, the list needs to be able to create list_iterators. Here’s how:
template<T> class list_iterator { ...
private:
list_iterator(list_element<T>* p)
: p_(p) {
}
friend class list<T>;
};
The friend declaration says list can reach into list_iterator’s private parts. It is common for iterators and collections to declare one another as friends, since they need mutual access.
Now the min_element code above just works. And it is as fast as a min_element loop on lists can be. This is absolutely magical.
Posted on February 17, 2012